1. Introduction
NLP를 다루는 많은 Application들은 매우 큰 PTLM을 여러 downstream task를 다루기 위해 adapting 방식을 사용했다. adaptation은 일반적으로 pre-trained model의 전체 파라미터를 update하는 fine-tuning을 사용했다. 하지만 점차 NLP에서 개발되는 모델들이 커지면서 이런 방법은 굉장히 비효율적이게 되었다. (GPT3만 봐도 175 billion개의 학습가능한 파라미터가 존재한다. 이를 모두 학습시킬려면 시간적으로도, 컴퓨팅 자원적으로도 비용이 굉장히 많이든다.)
따라서 위와 같은 fine-tuning 방식을 피하기 위해 몇 개의 파라미터만을 adapting하거나 외부 모듈을 학습하는 방식이 계속 연구되고 있다. (Ex. adapter module) 이런 방식을 사용하면 task-specific parameter(task에 종속된 파라미터)가 적기 때문에 각 task마다 이러한 파라미터를 기존 pre-trained model에 추가만 해주면 된다. (save and load에 유용하다.) 하지만 기존에 나온 기법들은 model depth를 늘려 inference latency가 발생되거나 모델의 입력 가능한 문장 길이를 줄여야했다. 또한 이러한 방법들은 efficiency와 model quality간의 trade-off를 고려하기 때문에 fine-tuning baselines에 맞지 않다.
논문 저자들은 over-parametrized model들이 실제로는 low intrinsic dimension(낮은 고유 차원)에 상주(reside)한다는 사실에 영감을 받았다고 한다. 저자들은 model adaptation동안 가중치 변화 역시 low "intrinsic rank"를 가진다고 가정하고 Low-Rank Adaptation(LoRA)를 제안한다.
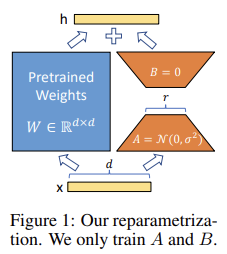
위 그림과 같이 LoRA는 pre-trained witght들은 frozen한다. 대신 adaptation동안 dense layer들의 변화에 대한 rank decomposition(차원 분해) matrices를 최적화함으로써 dense layer들을 간접적으로 학습시킨다. 논문에서는 GPT-3의 경우 full rank (전체 차원)이 12,288정도인데, 매우 적은 차원인 1~2차원으로 낮춰도 (low rank로 낮춰도) 충분했다고 한다. (덕분에 storage 효율과 compute 효율을 높일 수 있다.)
LoRA의 핵심 advantage는 다음과 같다.
- pre-trained model은 다른 테스크에 사용될 많은 LoRA module을 만들기 위해 공유되고, 사용될 수 있다. pre-trained model의 공유된 부분은 frozen되기 때문에 수행할 테스크를 바꿀 경우 단지 Figure1에서의 A와 B 두 가지 matrix를 바꾸면 된다. 덕분에 strage requirement와 task-switching overhead를 상당히 줄일 수 있다.
- LoRA는 adaptive optimizer를 사용할 때 gradient 계산을 할 필요가 없고, 대부분의 파라미터들에 대한 optimizer를 유지할 필요도 없다. 이 덕분에 훈련이 더 효율적이고, 하드웨어 진입 장벽이 3배 감소했다. 대신 추가된 low-rank matrix들을 최적화했다고 한다.
- Inference latency가 발생하지 않는다.
- LoRA는 이전 기법들과 직교(orthogonal)하기 때문에 prefix-tuning 등과 함께 사용될 수 있다. (combine될 수 있다.)
2. Problem Statement

위 수식은 기존의 full fine-tuning을 나타내는 식이다. 해당 수식에 대한 논문 내용은 다음과 같다.
- PΦ(y|x): pre-trained autoregressive language model이다. Φ로부터 parametrized된다.
- x, y의 의미를 살펴보자. 예를 들어, 자연어를 SQL로 바꾸는 NL2SQL 테스크를 생각해보자. 이때 natural language는 x가 되고, x에 짝이 되는 SQL문은 y가 되는 것이다.
- full fine-tuning을 하기 전 모델은 pre-trained wieght인 Φ0으로 초기화 된다. 이후 fine-tuning이 진행되면서 Φ0+∆Φ로 값이 갱신된다.
- 이때 가장 큰 문제는 각각의 downstream task에 대해 fine-tuning을 진행할 때 항상 다른 parameter set인 ∆Φ를 학습해야 한다. 이때, ∆Φ의 크기는 Φ0의 크기와 동일하다. 즉, GPT-3의 경우 Φ0의 크기가 175Billion 정도인데, 이 크기와 비슷한 양의 파라미터를 학습해서 저장하고 있어야 한다.

그래서 해당 논문에서는 더 parameter-efficient한 접근법을 채택했다고 한다. 이때 ∆Φ는 ∆Φ(Θ)와 동일하다. 즉, ∆Φ를 찾는 테스크는 Θ를 optimize하는 것과 동일한 테스크가 된 것이다. Θ는 훨씬 작은 크기의 파라미터로 Φ0보다 훨씬 작다. 해당 논문에서는 ∆Φ를 encode하기 위해 low-rank representation을 제안했다고 한다. 해당 방법은 compute- and memory-efficient하다. (GPT3의 Φ0는 175B이지만 실제로 trainable parameter 개수인 |Θ|의 크기는 해당 크기의 0.01%밖에 되지 않았다.)
3. Arent't Existing Solutions Good Enough?
NLP 분야에서는 transfer learning을 위해 크게 두 가지 방식을 사용했다.
- adapter layer를 추가하는 방식
- input layer activation들의 form을 optimize하는 방식
그러나 두 가지 방식은 다음과 같은 제약이 있다.
- Adapter layers Intoduce Inference Latency (Adapter 방식의 제약)
- Directly Optimizing the Prompt is Hard (Prefix tuning 방식의 제약)
4. LoRA Method
4.1. Low-Rank-Parametrized Update Matrices
neural network는 matrix multiplicaiton을 수행하는 많은 dense layer들을 가진다. 이때 이 layer들의 weight matrix들은 모두 full-rank를 가진다. 이전 연구에 따르면 특정 테스크에 adapting할 때 pre-trained language model들은 low "instrisic dimension"을 가짐을 보여줬다. 그리고 더 작은 subspace로 random proejction함에도 불구하고 효율적으로 학습할 수 있음을 밝혔다. 이것에 영감을 받아 논문 저자들은 가중치 갱신 역시 adaptation과정에서 low "instrisic dimension"을 가진다고 가정한다.
- Random Projection: 고차원의 데이터를 저차원의 특징 공간으로 표현하는 방법.
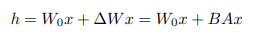
pre-trained weight matrix인 W0가 d×k의 차원을 가진다고 하자. 이때 우리는 이를 specific task에 적용하기 위해 update를 하려고 하면 W0+∆W를 사용해야할 것이다. (위에서 말한 수식과 동일하다.) 이때 우리는 low-rank decomposition을 활용해 B를 d×r 차원, A를 r×k 차원으로 표현하여 W0+∆W = W0+AB로 표현할 수 있다. 이때 rank r은 min(d, k)보다 훨씬 작은 값을 사용한다. 학습이 되는 동안 W0는 frozen되며 gradient update를 받지 않는다. (A, B는 trainable parameter이다.)
- W0와 ∆W=AB는 동일한 input 값으로 multiple된다. 그리고 이 둘 각각의 output vector는 coordinate-wise 방식으로 sum연산이 수행된다. (좌표값에 맞게 더해진다.)

Figure1에서 A는 random Gaussian initialization을 수행하고, B는 zero로 초기화한다. 따라서 학습 시작때 ∆W(=AB)는 0이다. 그리고 ∆Wx를 a/r로 scaling한다. (이때 a는 r의 상수이다.) Adam으로 optimizing을 할 때, initialization을 적절히 scale하면, a를 tuning하는 것은 learning rate를 tuning하는 것과 동일하다. 결과적으로, 처음 r에 대해 a를 간단히 설정하고, 이후 이 값은 tuning할 필요가 없다. 이 scaling 과정은 다양한 r에 대해 hypterparmeter들을 다시 tuning할 필요를 줄여준다.
4.2. Applying LoRA To Transformer
transformer architecture에는 self attention module에 네 가지 weight matrix들이 존재한다(Wq, Wv, Wk, Wo).
- Wq는 query, Wv는 value, Wk는 key, Wo는 output에 대한 wegith matrix를 의미한다.
- Wq, Wk ,Wv는 self-attention이므로 모델의 임베딩 차원수를 d_model이라고 하면 차원의 크기는 d_model×d_model이 된다.
LoRA는 trainable parameter 수를 줄이기 위해 neural network의 어떠한 weight matrix들의 subset도 상관없이 적용가능하다. 따라서 저자들은 transformer의 경우 MLP module 부분은 froze시키고 attention weight 부분만 adapting하도록 제한했다.
LoRA의 Benefit은 다음과 같다
- The reduction in memory and storage usage.
- We can switch between tasks while deployed at a much lower cost. (LoRA weigh 부분들만 바꿔주면 되기 때문이다.)
Limitation은 다음과 같다.
- It is not straightforward to batch inputs to different tasks with different A and B in a single forward pass, if one chooses to absorb A and B into W to eliminate additional inference latency.
→ 추가적인 inference latency를 없애기 위해 W로 a, b가 흡수되도록 했다면, single forward pass(단일 순방향 패스)에서 다른 A와 B를 가진 (다른) 여러 작업들의 input을 batch처리하기 어렵다.
5. Empirical Experiments
LoRA는 기존 가중치 행렬과 parallel하게 훈련할 수 있는 여러 rank decomposition matrix 쌍들을 추가한다. (논문에서는 Wq와 Wv에만 적용했다.) trainable parameter의 개수는 rank r과 기존 가중치의 shape에 의해 결정된다. 식으로 표현하면 다음과 같다.

이때 L_LoRA는 LoRA를 적용하는 가중치 행렬의 개수를 의미한다.
이후 여러 결과들이 나오는데 해당 결과들은 논문을 참고하고 그중 몇 가지 중요한 결과들에 대해서만 살펴보자.
5.1. Which Weight Matrices In Transformer Should We Apply LoRA To?
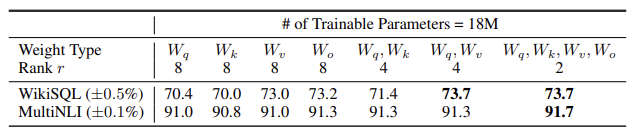
논문 저자들은 downstream task의 best performance를 뽑아내기 위해 LoRA를 어떻게 적용하면 좋은지 확인했다. 단, GPT-3에서 trainable parameter를 총 18M 정도로 제한했다고 한다. 이때 하나의 attention wight type에 대해서만 adapt하는 경우 r은 8, 두 종류에 대해 adapt하는 경우는 4, 모든 것을 대상으로 하는 경우는 2로 설정했다고 한다. 결과를 정리하면 아래와 같다.
- ∆Wq 혹은 ∆Wk를 사용하는 경우 가장 낮은 성능을 보였다.
- ∆Wq와 ∆Wv를 사용하는 경우 가장 좋은 성능을 보였다.
→ 이는 rank를 4로 설정해도 ∆W에 대한 충분한 정보를 가지고 있음을 보여준다.
5.2 What Is The Optimal Rank r For LoRA?

그리고 저자들은 rank r이 model performance에 미치는 영향을 확인했다. 결과는 다음과 같다.
- r을 증가시킨다고 해서 더 의미있는 subspace를 cover하진 않는다. 따라서 low-rank adaptation matrix로도 충분하다.
아래는 r=8일 때와 r=64일 때 SVD를 적용하여 얻어낸 right-singular unitary matrice를 통해 유사도를 정량화한 것이다.

- 상위 singular vector를 겹쳐보면 r=8인 경우와 r=64인 경우 모두 상당히 겹침을 확인할 수 있다.
- 위 그림은 상위 singular vector들은 상당히 유용함을 보여준다. 하지만 direction으로는 학습 중에 점점 random noise가 쌓임을 알 수 있다. 따라서 adaptation matrix는 매우 작은 rank를 가져도 된다.
출처
논문: https://arxiv.org/pdf/2106.09685
'AI > NLP' 카테고리의 다른 글
| [논문 리뷰] Prefix-Tuning: Optimizing Continuous Prompts for Generation (0) | 2024.05.03 |
|---|---|
| [논문 리뷰] Parameter-Efficient Transfer Learning for NLP (Adapter) (0) | 2024.05.01 |
| Parameter Efficient Fine-Tuning (PEFT)란? (0) | 2024.04.30 |
