[백준] 6549: 히스토그램에서 가장 큰 직사각형 (python 파이썬)

히스토그램은 직사각형 여러 개가 아래쪽으로 정렬되어 있는 도형이다. 각 직사각형은 같은 너비를 가지지만, 높이는 서로 다를 수 있다. 아래는 높이가 2, 1, 4, 5, 1, 3, 3이고 너비가 1인 직사각형으로 이루어진 히스토그램이며 색칠된 부분은 가장 넓은 직사각형이다.

 

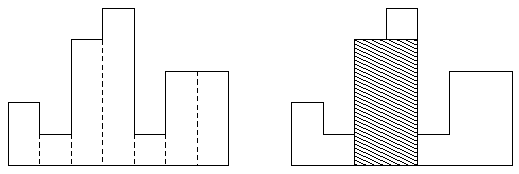
위와 같이 가장 넓은 직사각형을 구하기 위해서는 다음과 같은 알고리즘을 적용할 수 있다. 이때 히스토그램의 각 부분(2, 1, 4, 5, 1, 3, 3의 높이를 가지는 객체)를 ‘막대기’라고 부르자. 

1. 모든 막대기 중에 가장 낮은 높이의 막대기를 선택한다. 
2. (가장 낮은 높이) × (막대기의 개수)를 통해 현재 히스토그램에서 가장 낮은 높이의 직사각형의 넓이를 구한다.
3. 가장 낮은 높이의 막대기를 기준으로 왼쪽과 오른쪽으로 나눈다.
4. 각 부분(왼쪽 or 오른쪽)의 가장 낮은 높이의 막대기를 선택하여 위 과정을 반복한다.
5. 지금까지 구한 막대기 중 가장 넓은 직사각형의 넓이를 반환한다. 

위 과정을 python 코드를 통해 작성하면 다음과 같다.

import sys
sys.setrecursionlimit(10**6)
input = sys.stdin.readline

def find_max_rectangle(left: int, right: int):
    if right < left: # left가 right보다 큰 경우 직사각형의 넓이가 될 수 없는 -1을 리턴한다.
        return -1
    
    # 가장 낮은 높이를 가지는 직사각형의 인덱스를 탐색한다.
    min_index = left 
    for index in range(left+1, right+1):
        if histogram[index] < histogram[min_index]:
            min_index = index
            
    min_height = histogram[min_index] 						  
    left_ractangle = find_max_rectangle(left, min_index-1)   # 왼쪽 부분에서 가장 큰 직사각형의 넓이를 구한다.
    right_ractangle = find_max_rectangle(min_index+1, right) # 오른쪽 부분에서 가장 큰 직사각형의 넓이를 구한다.
    
    # 현재 탐색하는 left~right 범위에서 가장 큰 직사각형을 구하고 이를 return한다.
    max_ractangle = max(min_height * (right-left+1), left_ractangle, right_ractangle)
    return max_ractangle

while True:
    input_values = list(map(int, input().split()))
    n = input_values[0] # n: 막대기의 개수
    
    if n == 0:          # 막대기의 개수가 0인 경우 테스트 종료
        break
    
    histogram = input_values[1:]
    max_ractangle = find_max_rectangle(0, n-1)
    print(max_ractangle)

하지만 위 알고리즘은 최선의 경우 계속 반씩 나뉘어 O(nlogn)만큼의 시간 복잡도를 가진다. 하지만 최악의 경우(즉, 가장 왼쪽 혹은 가장 오른쪽 막대기가 계속 가장 낮은 높이로 선정되는 경우) 총 n번 탐색해야 하므로 O(n²)의 시간 복잡도를 가진다. 이때 위 문제에서 n은  1 ≤ n ≤ 100,000의 시간 복잡도를 가지므로 최악의 경우에는 시간 제한 1초 내에 문제를 풀 수 없다. (실제로 위 코드로 제출 시 시간 초과로 오답이 나온다.)

 

이 문제를 해결하기 위해 무조건 O(nlogn)으로 해결 할 수 있는 분할 정복법을 생각해봤다. 방법은 아래와 같다.

1. 탐색하고자 하는 범위(left~right)의 중앙 인덱스를 가져온다.
2. 중앙 인덱스를 mid라고 할 때, mid, mid+1 번째 막대기 중 낮은 높이(min_height)를 선택하여 2×min_height를 수행한다.
3. 이후 mid의 왼쪽 막대기, mid+1의 오른쪽 막대기 중 더 높은 높이의 막대기를 가져오고, 3개의 막대기 중 가장 낮은 높이(min_height)를 선택한다. 그리고 3×min_height를 수행하여 2번에서 구한 직사각형의 넓이와 비교하여 더 넓은 직사각형의 넓이를 저장한다.
4. 왼쪽과 오른쪽으로 위와 같은 방식으로 계속 확장하면서 동일한 과정을 거치며 가장 넓은 직사각형의 넓이를 구한다.
5. 중앙 인덱스(mid)를 기준으로 왼쪽과 오른쪽으로 나누어 2~4번 과정을 동일하게 반복한다. 단, left가 right와 동일한 경우 현재 존재하는 단 하나의 막대기의 넓이를 반환한다.
6. 왼쪽, 오른쪽에서 구한 최대 넓이와 현재 범위에서 구한 최대 넓이를 비교해 가장 넓은 직사각형의 넓이를 반환한다.

위 알고리즘은 항상 탐색하는 범위가 반으로 나뉘는 것을 보장하고, 분할 트리의 각 높이 마다 n번의 탐색이 수행되므로 최선, 최악의 경우 모두 O(nlogn)을 보장한다. 이를 python 코드로 구현하면 다음과 같다.

 

import sys
sys.setrecursionlimit(10**6)
input = sys.stdin.readline

def find_max_rectangle(left: int, right: int):
    if left == right:
        return histogram[left]
    
    mid = (left+right)//2 
    width = 2
    min_height = min(histogram[mid], histogram[mid+1])
    max_ractangle = min_height*width
    
    # 위에서 설명한 알고리즘을 수행한다.
    # i: 왼쪽을 확장할 때 쓰는 인덱스를 i, 오른쪽을 확장할 때 쓰는 인덱스를 j로 선언한다. 
    i = mid; j = mid+1    
    	while left < i or j < right: # i가 left까지 혹은 j가 right까지 확장되지 않았다면
        # 오른쪽으로 더 이상 확장될 수 없거나, 왼쪽을 확장할 수 있을 때 다음에 확장될 왼쪽의 막대가 확장될 오른쪽 막대보다 크거나 같은 경우
        if j == right or (left < i and histogram[i-1] >= histogram[j+1]):             
        	i -= 1
            width += 1
            min_height = min(min_height, histogram[i])
            max_ractangle = max(max_ractangle, min_height*width)
        # 왼쪽으로 더 이상 확장될 수 없거나, 오른쪽으로 확장할 수 있을 때 다음에 확장될 오른쪽 막대가 왼쪽 막대보다 큰 경우
        else:
            j += 1
            width += 1
            min_height = min(min_height, histogram[j])
            max_ractangle = max(max_ractangle, min_height*width)
    
    # 지금까지 탐색한 최대 직사각형 넓이와 왼쪽, 오른쪽 부분 각각의 최대 직사각형 넓이 중 가장 큰 값을 반환한다. 
    max_ractangle = max(max_ractangle, find_max_rectangle(left, mid), find_max_rectangle(mid+1, right))
    return max_ractangle
    

while True:
    input_values = list(map(int, input().split()))
    n = input_values[0]
    
    if n == 0:
        break
    
    histogram = input_values[1:]
    max_ractangle = find_max_rectangle(0, n-1)
    print(max_ractangle)

 

https://www.acmicpc.net/problem/6549

6549번: 히스토그램에서 가장 큰 직사각형